Hi All,

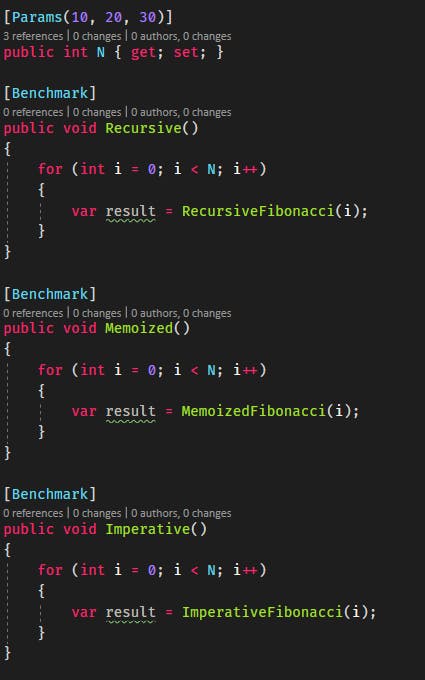
Today I want to share a small tip about how to speed up our function by memoization. Memoization is basically saving your function result with the provided arguments. If you call again your function with the same arguments, the result will be taken from the cache instead of executing the function again. The code I provided will be in C# but it is easy to implement in other languages as well. I also make benchmarks via the Benchmark.NET NuGet package. I will share a screenshot of the performance result at the end. Enough talk let's jump into the code :)

//classic recursive solution to Fibonacci. Nothing new here
public int RecursiveFibonacci(int num)
{
    if (num < 0)
    {
        throw new ArgumentException("number must be >= 0");
    }
    if (num < 2)
    {
        return num;
    }
    return RecursiveFibonacci(num - 1) + RecursiveFibonacci(num - 2);
}

//With C# 8 we can use inline functions. Here internal inline function
//can access outside variable memo hash. It will first check if the result
//presents in hash otherwise first calculate the result and then  add to the
//hash(You can easily implement this in Javascript via closures) 
public int MemoizedFibonacci(int num)
{
    if (num < 0)
    {
        throw new ArgumentException("number  must be >= 0");
    }
    var memo = new Dictionary<int, int> { { 0, 0 }, { 1, 1 } };
    return internalFibonacci(num);

    int internalFibonacci(int num)
    {
        if (memo.ContainsKey(num))
        {
            return memo[num];
        }
        var value = internalFibonacci(num - 1) + internalFibonacci(num - 2);
        memo[num] = value;
        return value;
    }
}

//Good, old and best way. No recursion, no fancy closures ...etc
//And of course the most performant function in benchmark results 
public int ImperativeFibonacci(int num)
{
    int start = 0, end = 1, count = 0;
    while (count++ < num)
    {
        int temp = end;
        end = start + end;
        start = temp;
    }
    return start;
}

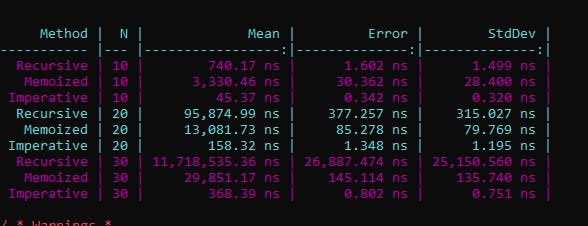
And here is the benchmark result

And my test codes are as below. Stay tuned.